【解説】2015神奈川県公立高校入試 数学-問2(オ)

こんにちは。数学を教えている深川です。
神奈川県公立高校入試の数学について気になる問題をテーマに
これからしばらく週2回を目標に解説を書いていきます。
関連記事
- 2015年神奈川県公立高校入試の問題傾向と難易度はこちら
- 問2の(カ)確率の解説はこちら
- 問2の(ク)円周角の解説はこちら
- 問3の二次関数のグラフの解説はこちら
- 問4の資料の整理の解説はこちら
- 問5の二次方程式の文章題の解説はこちら
今回は問2の(オ) 変化の割合の定番の問題です
神奈川県平成27年度:問2(オ)
関数 y = ax^2 について、x の値が -3 から -1 まで増加するときの
変化の割合が -3 であった。このとき a の値を求めなさい。
(「^2」という表現は2乗を表現しています。)
しっかり勉強してきた人にとって、この問題は定番でしょう。
まずは変化の割合の求め方をはっきりと意識する解き方。
変化の割合は、
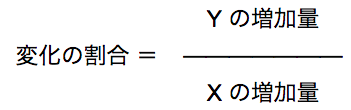
で求めることができます。
「 x の増加量 ぶんの y の増加量」と呪文のように唱えて覚えてください。
このことから以下のようにして解けます。
y = ax^2 について、
x = -1 のとき y = a
x = -3 のとき y = 9a
なので、
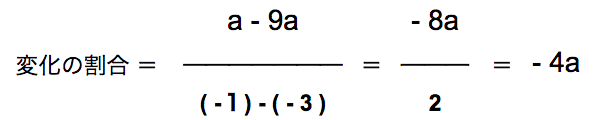
変化の割合は -3 なので、
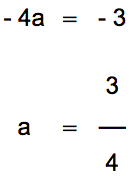
言葉の定義に沿って解くこの方法を僕は好きです。
しかし受験は準備が勝負です。
定番の問題には素早い解法を用意しておいたほうがよいでしょう。
もっと早い解き方がある!
中学数学の範囲では二次関数のグラフの頂点は必ず原点を通ります。
この条件を満たしている二次関数では、
変化の割合は以下の公式で求めることが出来ます。
二次関数上の2点 P、Q の X 座標をそれぞれ p 、q とすると、
変化の割合 = a( p + q )
この公式を使って改めて問題を解くと、
変化の割合 = a { (-1) + (-3) } = -4a
変化の割合は -3 なので、
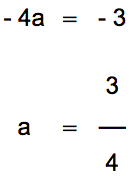
先ほど紹介した変化の割合の求め方より、随分とスッキリしましたね。
なぜ同じ答えになるの?
数学の指導をしていてこのような公式を紹介する際に感じて欲しいことは、
「なぜ?」です。
なぜ、
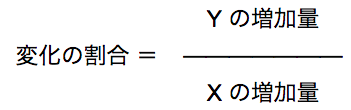
を使って出した答えと同じになるのか?
今回はたまたま同じ値になっただけで、違うこともあるんじゃないか?
公式や定理に対して、いつもそういった気持ちで向き合ってほしいですね。
次にやるべきことは確認です。僕が紹介した公式は間違っているかもしれません。確認(証明)しましょう。
紹介した公式が使える場合は、二次関数のグラフの頂点が原点と一致するものに限っているので、二次関数は以下のように一般化できます。
y = ax^2( a は任意の実数)・・・(あ)
a の説明に「任意の~」と書いています。任意というのは数学ではよく使われる言葉で、「適当な数を当てはめてください」と、書いてあると思ってください。
y = ax^2( a は適当な実数)
a の部分を1や2、-3などの具体的な数を使わないのは、グラフの頂点が原点と一致するあらゆる二次関数を表現するためです。
「あらゆる~」について考えられるようにすることを一般化と言います。
(あ)のグラフ上にある2点 P、Q の X 座標をそれぞれ p 、q とすると、
P( p , ap^2)
Q( q , aq^2) となるので、
変化の割合は、
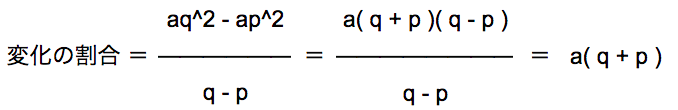
これで「 x の増加量 ぶんの y の増加量」に従って、
変化の割合 = a( p + q ) という式を導くことが出来ました。
ここまで確認、理解して、受験で使えるようこの公式を使い込んで下さいね。
私たちは、横浜にある小さな個別指導の学習塾です。
受験をはじめとした勉強において、固定的なカリキュラムや決まった勉強方法に生徒を適応させることに意識が向きがちです。
私たちはそれらを大切にすると同時に「生徒」を中心とした学習方法を提案し実践することが、生徒が勉強を楽しむことに繋がり、学力の向上につながると考えています。
「自分に合ったやり方で勉強したい」「どうせやるなら勉強を好きになってもらいたい」という方は是非ティーシャルをご検討ください。


