【解説】2015神奈川県公立高校入試 数学-問2(カ)

こんにちは。数学を教えている深川です。
神奈川県公立高校入試の数学について気になる問題をテーマに
これからしばらく週2回を目標に解説を書いています。
関連記事
- 2015年神奈川県公立高校入試の問題傾向と難易度はこちら
- 問2の(オ)変化の割合の解説はこちら
- 問2の(ク)円周角の解説はこちら
- 問3の二次関数のグラフの解説はこちら
- 問4の資料の整理の解説はこちら
- 問5の二次方程式の文章題の解説はこちら
今回は問2の(カ) 確率の典型問題です
神奈川県平成27年度:問2(カ)
1から6までの目がでる大、小2つのサイコロを同時に1回投げるとき、出た目の数の和が9以上とならない確率を求めなさい。ただし大、小2つのサイコロはともに1から6までのどの目が出ることも同様に確からしいものとする。
この問題は定期テストで出されるような問題ですね。つまり易しいです。
まず問題文の解釈ですが、
9以上とならない確率という表現でミスをする人はいるかもしれませんね。
「8以下となる確率」と解釈したほうが間違いが減るでしょう。
確率は以下の式で求まります。

「全体の」という意味は「起こりうる全ての」という意味です。
ちなみに「場合の数」という表現は「事象」という表現に
置き換えられることもあります。
全体の場合の数は、
大きなサイコロの目の出方が6通り、
小さなサイコロの目の出方が6通りなので、
全体の場合の数 = 6 × 6 = 36通りです。
2つのサイコロを投げる問題であれば表を使えば解けます。
このような表を書きます。

この表は一番上は小さなサイコロの目、一番左は大きなサイコロの目を表しています。その他のマスは2つのサイコロの目の和です。和を表すマスは36通りあるので先ほどの計算とも一致していますね。
次に8以下の数を書いたマスに何か印を付けてください。
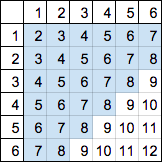
あとは印を付けたマスがいくつあるのかを数えれば、
条件を満たした場合を数えたことになります。
条件を満たす場合の数は26なので、
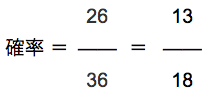
これが答えです。
さて。なんとなくこのマス目の数が斜め一直線に並んでいる感じが、
「すごくいい。」なんて思ったりしませんか?
思えちゃう人はきっと数学の素質があります。
「なったからそうなんだろう。」とスルーしてしまうともったいないです。
小さなサイコロの目を X 、大きなサイコロの目を Y 、その和を S とすると、
X + Y = S となります。( S とするのは一般化のためですね。)
式変形すると、
Y = – X + S となります。
この式どこかで見たことありませんか? そうです。一次関数です。もう一度表を確認してみましょう。今度はサイコロの目であることは忘れて、横軸が X 、縦軸が Y だと思って下さい。

グラフは点で X 、Y を表現しますが今回はマス目で表現したと思って下さい。すると一直線になる理由も納得出来るのではないでしょうか?
試しに、X + Y = 5 つまり、Y = – X + 5 を見てみると、
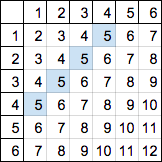
となります。シンプルだけど整ってる感じがいいですね。
よく観察すると、Y = – X + S の傾きは -1 なのに数字の並びの傾きは 1 ですね。おかしいです。
実はグラフの Y軸の向きが下の図のように上下逆なんです。
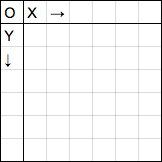
Y軸が下向きが正の向きなので、傾きも逆転しています。
ちなみに X = 0 、Y = 0 のマスに原点を表す O を入れておきました。
問題は「和が8以下」が条件だったので、それを素直な式にすると
X + Y ≦ 8 となります。
これを満たすマスのゾーン(領域)に色を塗ったと言えます。
※グラフの広さのある場所のことを「領域」と高校数学では表現します。広さのない場所は「点」ですね。

今回はサイコロの和についての問題でした。
積の場合だと表がどんな模様になるのか考えてみて下さいね。
私たちは、横浜にある小さな個別指導の学習塾です。
受験をはじめとした勉強において、固定的なカリキュラムや決まった勉強方法に生徒を適応させることに意識が向きがちです。
私たちはそれらを大切にすると同時に「生徒」を中心とした学習方法を提案し実践することが、生徒が勉強を楽しむことに繋がり、学力の向上につながると考えています。
「自分に合ったやり方で勉強したい」「どうせやるなら勉強を好きになってもらいたい」という方は是非ティーシャルをご検討ください。


