【解説】2015神奈川県公立高校入試 数学-問5

こんにちは。数学を教えている深川です。
神奈川県公立高校入試の数学について気になる問題を解説しています。
関連記事
- 2015年神奈川県公立高校入試の問題傾向と難易度はこちら
- 問2の(オ)変化の割合の解説はこちら
- 問2の(カ)確率の解説はこちら
- 問2の(ク)円周角の解説はこちら
- 問3の二次関数のグラフの解説はこちら
- 問4の資料の整理の解説はこちら
第6回目は問5です
工場Aでは、製品Pの出荷数について、
1年目に100個出荷し、
2年目には1年目よりa割多く出荷し、
3年目には2年目より2a割多く出荷する計画を立てた。このとき、次の問②答えなさい。
(ア)a = 1 のとき、工場Aにおいて、2年目に出荷する製品Pの個数を求めなさい。
(イ)工場Aにおいて、3年目に製品Pを208個出荷するとき、
aについての方程式をつくり、aの値を求めなさい。
ただし a > 0 とする。なお、答えを導くまでの途中過程も書きなさい。
※本物の問題は文字 x を使用していますが 、解説で掛け算の記号と混同しないよう a を使用します。
問5は二次方程式の問題です。問3、4よりも簡単な印象です。
学校の定期テストで方程式の単元を8割得点できる実力があるなら、
この問題はミスせず解けるのではないでしょうか。
普通に解ける人も多いでしょうから、丁寧に噛み砕いて解説したいと思います。
数量をどう文字式で表すか
文章題を方程式で解くためのコツは、登場する数量をどう文字式で表すかです。
1年目、2年目、3年目の出荷数を文字式で表してみます。
といっても1年目の出荷数は100個と決められているので、文字は使いませんね。
2年目には1年目よりa割多く出荷するそうです。
「1年目より a割多い」という数量を a を使って表すとどうなるでしょうか?
まず具体的に数字を当てはめて考えてみます。
a = 3 だとして「1年目の 3割」の部分を考えると、
その数量は 100 × ( 3 / 10 ) = 30(個)です。
「100 の3割が 30」というのはしっくりくるのではないでしょうか?
「~割」という割合の表現は、10割が元にする量の全体を表します。
a が 10 に対してどれぐらいの大きさかを式にすると「 a / 10 」となります。
よって「1年目の a割」を a を使って表すと、
100 × ( a / 10 ) = 10a となります。
「1年目の a割」が 10a個なら、
「1年目より a割多い」というのはどのように考えればよいか。
この場合もまず具体的に数字を当てはめて考え易くしましょう。
「1年目より 3割多い」という表現について考えます。
3割という割合の表現が含まれているので、元にする数が必要です。
このあたりの理解は数学力というよりも国語力ですが、
「1年目より 3割多い」→「1年目より、1年目の 3割多い」と解釈しましょう。
だからこのようなイメージを持って下さい。

このイメージを式にすると、
「1年目」+「1年目の 3割」=「1年目より、1年目の 3割多い」です。
だから 100 + 30 = 130 となります。
「1年目より a割多い」を改めて考えると、
「1年目」+「1年目の a割」=「1年目より、1年目の a割多い」となります。
1年目 :100個
1年目の a割 :10a個 なので、
「1年目より a割多い」は、100 + 10a(個)となります。
大変解説が長くなりましたが、この数量が2年目の出荷数です。
3年目はどうなる?
3年目も文字式で表します。
3年目は2年目よりも 2a割多いそうです。
2年目が 100 + 10a(個)だったので、その 2a 割多いとなると・・???
100 + 10a(個)という部分がややこしく感じるので、
A = 100 + 10a(個)として置き換えて、シンプルに考えてみます。
「2年目よりも 2a割多い」を「2年目より、2年目の 2a割多い」と考えて、
下のようなイメージを持って下さい。

「2年目」はA個です。
「2年目の 2a割」は A × ( 2a / 10 ) 個です。
よって「2年目より、2年目の 2a割多い」は、
A + A × ( 2a / 10 )個 となります。
ここまできたら、A を 100 + 10a に戻しましょう。
100 + 10a + ( 100 + 10a )( 2a / 10 )
そして整理しました。
2a^2 + 30a + 100
これで2年目、3年目を a を使って表すことが出来ました。
文字式が分かれば解くのはカンタン!
それでは小問を考えていきましょう。
(ア)a = 1 のとき、工場Aにおいて、2年目に出荷する製品Pの個数を求めなさい。
2年目に出荷した製品Pの個数を求めたいので、
100 + 10 a に a = 1 を代入します。
100 + 10 × 1 = 110(個)
(イ)工場Aにおいて、3年目に製品Pを208個出荷するとき、
aについての方程式をつくり、aの値を求めなさい。
ただし a > 0 とする。なお、答えを導くまでの途中過程も書きなさい。
記述の問題形式ですね。
3年目の出荷数を a を使って表したものをいきなり書くと減点されるでしょうから、
「2年目が~なので、3年目は・・・である。」という具合に、
2年目をこう考えましたよ、と採点者に教えてあげるといいでしょう。
さて、3年目は 2a^2 + 30a + 100(個)なので、
2a^2 + 30a + 100 = 208 という方程式が成り立ちます。
208 を移項し、両辺を2で割ると、
a^2 + 15a – 54 = 0 となります。
これを解の公式を使って解きます。
解の公式は教科書(僕が確認したのは東京書籍)に導き方が説明されているので、
ここでの解説は割愛します。
すると、a = – 18 , 3 という解が求まります。
問題文には a > 0 という条件を与えられているので、a = 3 が答えです。
たすき掛けが便利
最近知りましたが、たすき掛けは公立中学校では習わないんですね。
たすき掛けとは二次式を素早く因数分解するテクニックです。
知らない人のためにたすき掛けを説明します。
※たすき掛けの説明の中の「 x 」は、すべて文字(エックス)です。
すでに因数分解された以下のような式があるとします。
( ax + b )( cx + d )
これを展開します。すると以下のような等式が成り立ちます。
( ax + b )( cx + d ) = acx^2 + ( ad + bc )x + bd
この式を観察すると x^2 の係数は ac 、定数項は bd なので、
例えば元の式が
αx^2 + βx + γ
といった式の場合、
α = ac 、γ = bd 、そして β = ad + bc を満たすような
a , b , c , d を考えなければなりません。
これを考えるためのアプローチがたすき掛けです。
下の図がたすき掛けの全体像です。
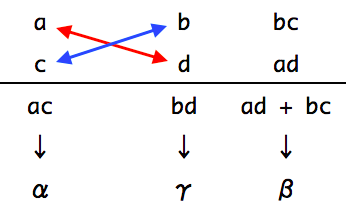
それではたすき掛けのやり方を説明します。
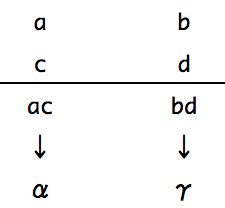
まず a , b , c , d に当てはめる数を、α = ac 、γ = bd の部分から推測します。
そして下の図のように書きます。ac 、bd の計算結果も書いておきましょう。
そして α = ac 、γ = bd を確認しておきます。
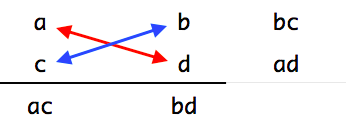
次に、a と d , b と c を掛け算します。
ばってんに掛けるところがたすき掛けの由来です。
最後に ad + cd が β と一致するか確認します。
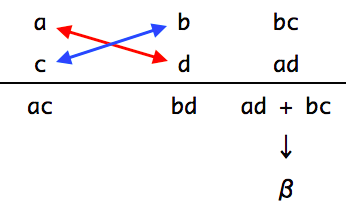
ちなみに一致しないこともよくあります。
その場合、最初の a , b , c , d から考え直さなければなりません。
たすき掛けで解く例
2x^2 – x – 6 という式で、たすき掛けを試してみます。
2 = 2 × 1
-6 = 3 ×(-2)
と考えて以下のように書きます。
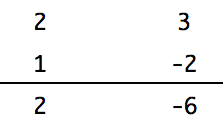
次に掛け算をします。
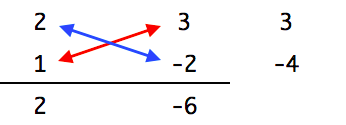
そして 3 – 4 = -1 を計算して、xの係数と一致していることを確認します。
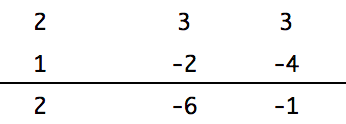
これで、2x^2 – x – 6 = ( 2x + 3 )( x – 2 ) と因数分解を計算することが出来ました。
繰り返しますがたすき掛けは今回のように1回で a , b , c , d を
求められるとは限りません。
それでもたくさん練習することで最初の推測の精度が上がり、
1回でたすき掛けの計算を成功させることが出来るようになります。
因数分解が遅いなら、たすき掛けを学んで特訓してみて下さい。
解の公式だけに頼るよりきっと素早く解けるようになります。
また、たすき掛けでルートを使うような場合は
解の公式を使ってしまった方が早いので、
そのあたりの勘も練習することで養って下さい。
以上解説でした。最後までお付き合いいただきありがとうございました。
私たちは、横浜にある小さな個別指導の学習塾です。
受験をはじめとした勉強において、固定的なカリキュラムや決まった勉強方法に生徒を適応させることに意識が向きがちです。
私たちはそれらを大切にすると同時に「生徒」を中心とした学習方法を提案し実践することが、生徒が勉強を楽しむことに繋がり、学力の向上につながると考えています。
「自分に合ったやり方で勉強したい」「どうせやるなら勉強を好きになってもらいたい」という方は是非ティーシャルをご検討ください。


